From Dictionary of Visual Words to Subspaces: Locality-constrained Affine Subspace Coding
Peihua Li, Xiaoxiao Lu, Qilong Wang
School of Information and Communication Engineering, Dalian University of Technology
peihuali@dlut.edu.cn, shaw,qlwang@mail.dlut.edu.cn
Abstract: The locality-constrained linear coding (LLC) is a very
successful feature coding method in image classification. It
makes known the importance of locality constraint which
brings high efficiency and local smoothness of the codes.
However, in the LLC method the geometry of feature space
is described by an ensemble of representative points (visual
words) while discarding the geometric structure immediately
surrounding them. Such a dictionary only provides a
crude, piecewise constant approximation of the data manifold.
To approach this problem, we propose a novel feature
coding method called locality-constrained affine subspace
coding (LASC). The data manifold in LASC is characterized
by an ensemble of subspaces attached to the representative
points (or affine subspaces), which can provide a piecewise
linear approximation of the manifold. Given an input descriptor,
we find its top-k neighboring subspaces, in which
the descriptor is linearly decomposed and weighted to form
the first-order LASC vector. Inspired by the success of usage
of higher-order information in image classification, we propose
the second-order LASC vector based on the Fisher information
metric for further performance improvement. We
make experiments on challenging benchmarks and experiments
have shown the LASC method is very competitive. |
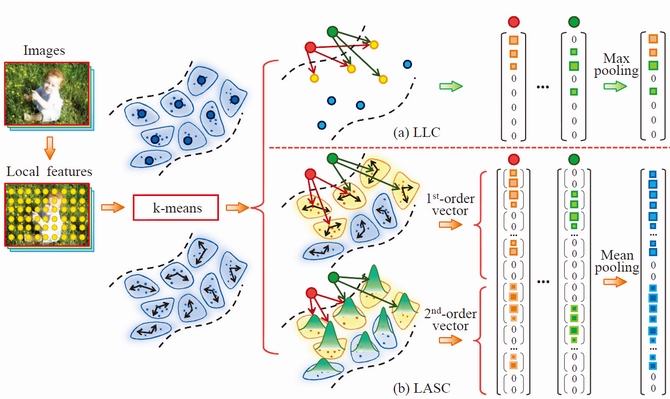
Figure 1. Locality-constrained affine subspace coding (LASC). The dictionary of LLC (a) is a set of representative points (visual words); the geometric structure immediately surrounding the words are discarded, and so it only provides a crude, piecewise constant approximation of the manifold. In contrast, the dictionary of LASC (b) is an ensemble of low-dimensional linear subspaces attached to the representative points (affine subspaces), which provides a piecewise linear approximation of the data manifold. For an input feature, we find its top-k nearest subspaces and perform linear decomposition of the feature in these subspaces weighted by the proximity measures. Beyond the linear coding, we propose to leverage the second-order information of the descriptors based on the Fisher information metric. Main results:
Paper: Peihua Li, Xiaoxiao Lu, Qilong Wang. From Dictionary of Visual Words to Subspaces: Locality-constrained Affine Subspace Coding. Int. Conf. on Computer Vision and Pattern Recognition (CVPR), 2015. [pdf] [bibtex] [code]
|
